Introduction

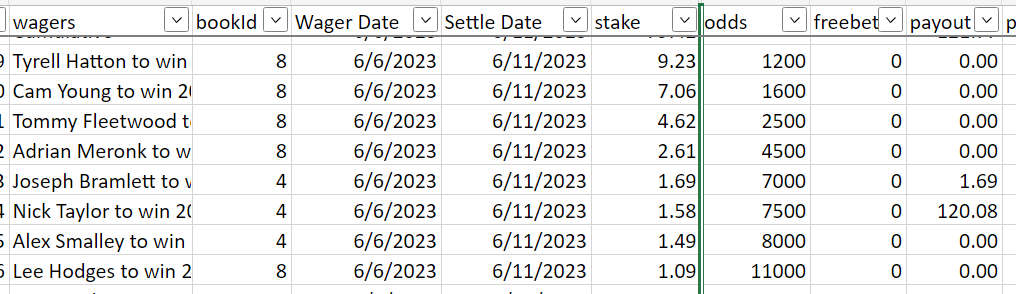
This year I’ve taken to gambling on pro golf tournaments, and one of my favourite markets to bet on is Tournament Outrights,ie: who is going to win the tournament. I’ll identify several players I like that week and construct a portfolio of outright bets from them.

Typically what I’ve done is first decide on a Payout Target I want to achieve should one of my wagers hit; at most one and only one of the wagers in the portfolio can hit because each wager is necessarily mutually exclusive. Then I work backwards to figure out what to wager on each player such that I’m agnostic to who specifically wins among them, since they would all payout the same. A recent example from the 2023 RBC Canadian Open,

You could equivalently lump all the individual bets together and treat them as one, “Hatton, or Young, or Fleetwood, …” etc. with +414 odds¹.

What has concerned me with this approach is that by setting the Payout Target first, the Total Stake (how much I am to wager) is then entirely decided by the odds I can get for the players in my portfolio. This has led to questionably large Stakes pre-tournament that I did not really intend for. This type of bet is not going to hit very often so I’d rather treat it as a lottery ticket; that a down 100% week is only a nominal sum and not substantial – at least in relation to the potential payout².

Fixing the Stake

Instead of setting the Payout Target and working towards the Total Stake, what if I did my process in the reverse. I begin by saying I only want to spend $ \(k\) and for all wagers \(\mathsf{w} = \{w_{1},w_{2},...\}\) in my portfolio, I want the payout to be the same in the event that one should hit. That is,

$$ \mathsf{max.} \quad w_{1}o_{1} $$ s.t.
$$ \sum_{w_{i} \in \mathsf{w}}{w_{i}} = k \ \forall i \neq j: w_{i}o_{i} = w_{j}o_{j} $$

where \(o_{i}\) is the odds in decimal format given for for wager \(w_{i}\). This is straightforward enough that it has an analytical solution,

$$ A\mathsf{w} = b \implies \mathsf{w} = A^{-1}b $$

provided that \(A\) is invertible, which it will be. The system of linear equations is,

$$ \begin{bmatrix} o_{1} & o_{2} & o_{3} & ... & o_{n} \\ o_{1} & -o_{2} & 0 & ... & 0 \\ o_{1} & 0 & -o_{3} & ... & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ o_{1} & 0 & 0 & -o_{n-1} & 0 \\ \end{bmatrix} \begin{bmatrix} w_{1} \\ w_{2} \\ w_{3} \\ \vdots \\ w_{n} \\ \end{bmatrix} = \begin{bmatrix} k \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} $$

and we just need to solve for \(\mathsf{w}\).

Interactive Bet Sizing Tool

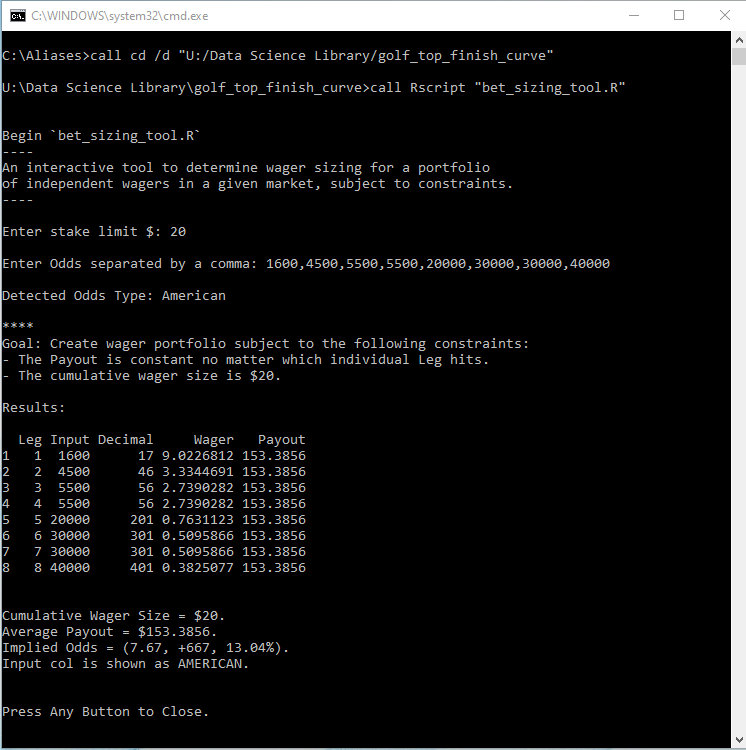
I put together a little interactive cmd line tool with R to help me construct my outright portfolio on the fly when I’m checking out the available odds early in the week. I give it the Total Stake, I give it the Odds and it spits out the solution to the system of linear equations above. For example, with the 3M Open this week I only wanted to spend $20 and I identified 8 players I liked,

And the tool returns the suggested portfolio to meet these constraints. We can then calculate the implied odds of the portfolio to be about +667 or ~13%.